Does a Rational Function Always Have an Asymptote

By Kur_272Bianca 18 May, 2022 Post a Comment

Approaches 0 as x increases. An asymptote is a line that the graph of a function approaches but never touches.

Math Scene Functions 2 Lesson 3 Rational Functions And Asymptotes

Rational functions then are functions written as fractions of polynomial functions in the form fx P x Q x where P x and Q x are polynomial functions.

. In this case f. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational numbersIn the case of one variable a function is called a rational function if and only if it can be written in the formwhere and are polynomial functions. Rx can only have a horizontal asymptote if.

What happens if you make x0 in the function. So what is an asymptote exactly. If lim x x 1 f x lim x x 2 f x is it guaranteed that f x will not pass through the horizontal asymptote.

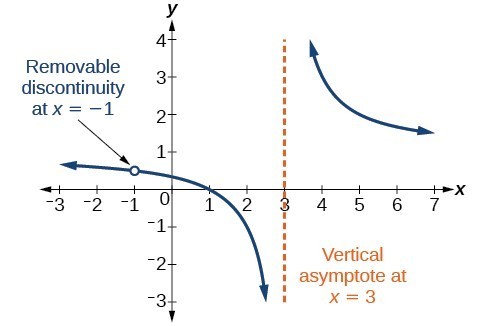
The answer to a good question about Rational Functions and AsymptotesDoes EVERY Rational Function Have a Vertical AsymptoteWhen would a rational function. A removable discontinuity might occur in the graph of a rational function if an input causes both numerator and denominator to be zero. In mathematics a rational function is any function which can be written as the ratio of two polynomial functions.

Rule 3 If the degree of the numerator is exactly one more than the degree of the denominator then the oblique asymptote is found by dividing the numerator by the denominator. Rational functions contain asymptotes as seen in this example. For example the factored function y x 2 x 3x 4 has zeros at x - 2 x - 3 and x 4.

The curves approach these asymptotes but never cross them. Y a b if the degree of the numerator P x is equal to the degree of denominator Q x where a is the leading coefficient of P x and b is leading coefficient of Q x. This time as long as m 0 the function has an oblique asymptote.

Learn how to find the verticalhorizontal asymptotes of a function. Asymptotes are ghost lines on a graph that either guide or shape the function or show where the function is undefined. Find the horizontal asymptote of Look at.

A rational function has at most one horizontal or oblique asymptote and possibly many vertical asymptotes. If nm then ya n b m is the horizontal asymptote. In a calculator you may get a divide by 0 error that is what happens when you touch a vertical asymptote bad things happen.

Asymptotes are lines that the curve approaches at the edges of the coordinate plane. The denominator cannot be equal to zero. If nm there is no horizontal asymptote.

If the quotient is constant then y this constant is the equation of a horizontal asymptote. This literally means that the asymptote is horizontal ie. The location of the horizontal asymptote is determined by looking at the degrees of the numerator n and denominator m.

Degree of Px Degree of. So the horizontal asymptote is th. As before the asymptote happens to be the same as the original linear.

Assume that q x has two distinct roots x 1 and x 2 where x 1 x 2 and the degree of p x is less that the degree of q x. Rational functions can have vertical horizontal or oblique slant asymptotes. A rational function can consist of a single number over a polynomial but not a polynomial over a single number.

Because because approaches 0 as x increases. To find the vertical asymptotes of a rational function we factor the denominator completely then set it. Rule 2 If the numerator and denominator have equal degrees then the horizontal asymptote will be a ratio of their leading coefficients.

The vertical asymptotes of a rational function will occur where the denominator of the function is equal to zero and the numerator is not zero. The rational function f x P x Q x in lowest terms has horizontal asymptote. Parallel to the axis of the independent variable.

Divide Nx by Dx. In other words vertical asymptotes occur at singularities or points at. Asymptotes of Rational Functions.

If n. Finding Horizontal Asymptotes of Rational Functions. Let f x be a rational function of the form p x q x where q x 0.

There is no horizontal asymptote. Your best bet is to make x a ridiculously small number to get an absurdly large answer. Rational functions can have 3 types of asymptotes.

Remember that an asymptote is a line that the graph of a function approaches but never touches. That is the ratio of the leading coefficients. We then use long division to find the oblique asymptote.

In this example there is a vertical asymptote at x 3 and a horizontal asymptote at y 1. Another way of finding a horizontal asymptote of a rational function. The graphs of rational functions are characterized by asymptotes.

Up to 8 cash back In a similar way mx b mx b1 is a rational function. Finding All Asymptotes of a Rational Function Vertical Horizontal Oblique Slant In this video we look at a function and find the vertical asymptote and also conclude that there are no horizontal asymptotes but that an oblique asymptote does exist. A rational function cannot touch the asymptote but why.

Following the usual procedure for finding the oblique asymptote of a rational function polynomial division we get y mx b as the asymptote. Vertical asymptotes occur only when the denominator is zero.

Graphs Of Rational Functions Horizontal Asymptote Video Khan Academy